1.1. 题目

1.1.1. 环形链表 II

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

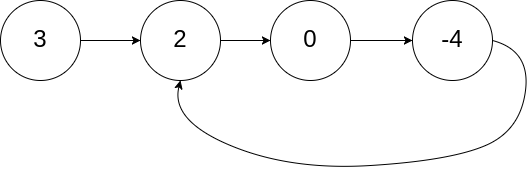
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

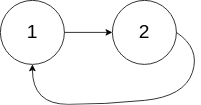
输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

1.1.2. 题解:

• 这题其实挺难的!因为得运用数学来解
• 首先,如果是环形,快慢指针肯定会相遇,而且快的指针是慢指针 跑过的距离的两倍!

1.1.3. 思路:

• 作弊做法(未实践): 就定一个指针,每次移动一步,把每个节点的地址存到map里,每走一个,校验一遍,map里key存地址,value存index,如果走到nil,那么没有环,如果遇到同一个地址,那么就是环入口了!
• 正常解法:
  • 首先,得理解如果正常环形链表什么时候相遇! 假设链表是个圆环! A B 两指针从原点0出发,当A到达圆环一半的时候,B应该回到了原点,当A到原点,正好一圈的时候,B也到了原点,两指针相遇
  • 如果像示例1一样的链表!那么依然还是快一圈相遇,不过不是入口原点! 可能往右偏移了几个点

    #                              .----.   
    #                             /      \  
    #      ___________X__________(O)     |(P) 
    #                             |      |  
    #                             \      /  
    #                              '----'   
    #                              (Y)
    

  • 假设 上图左侧非环形链表的长度为X,O表示环形入口处! 环整体长度为Y,然后假设快慢指针在P处相遇,OP距离为 L,P到原点的距离为PO为 J
  • 相同时间,快指针速度是慢指针的两倍,所以快指针走过的路程肯定也是慢指针的两倍 (速度 * 时间 = 距离)
  • 慢指针走 X + L, 那么快指针走过的距离 是慢指针的两倍 即 2(X + L)
  • 快指针走过的路线是 X + N(L+J) + L,其中 N 为 n圈
  • 那么 2X + 2L = X + N(L+J) + L
  • 得出 X = N(L + J) - L, 正好 L + J 是等于环的长度
    • 这地方理解有点绕, X 为 n圈 再减掉 一个 L的距离,假设 现在有个指针从P点开始,一次一步的进行往后移动,移动了N圈之后,回到P点,此时P点减掉 L 个节点,就是原点
  • 那么当相遇的时候,把快指针变成一次走一步,然后另外一个指针从开始的位置走,最后相遇的点肯定就是O点,也就是原点即环形入口的点了

1.1.4. 代码:

 func detectCycle(head *ListNode) *ListNode {
     // 如果直接nil或者下一个节点为nil,那么就肯定没有环了
     if head == nil || head.Next == nil {
         return nil
     }

     // 定义两个节点,一个为快指针,一个慢指针
     fast := head
     slow := head
     for fast.Next != nil && fast.Next.Next != nil {
         // 快指针肯定跑得快,快指针如果走到了nil,那么说明没有环
         if fast.Next == nil {
             return nil
         }
         // 快指针每次跳两步
         fast = fast.Next.Next
         // 慢指针每次跳一步
         slow = slow.Next
         // 当 快指针和慢指针相遇了
         if fast == slow {
             // head 节点开始走,fast指针改成每次走一步,相遇的时候 就是环形的起点
             for head != fast {
                 head = head.Next
                 fast = fast.Next
             }
             return head
         }
     }
     return nil
 }