1.1. 题目
1.1.1. 二叉树的垂序遍历
给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。
对位于(row, col)的每个结点而言,其左右子结点分别位于(row + 1, col - 1)和(row + 1, col + 1) 。树的根结点位于 (0, 0) 。
二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
返回二叉树的 垂序遍历 序列。
示例 1:
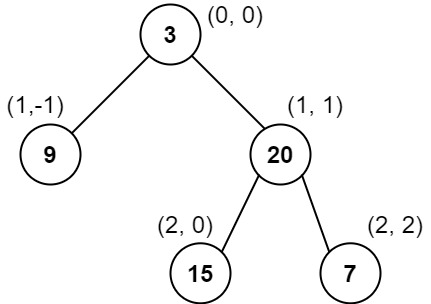
输入:root = [3,9,20,null,null,15,7]
输出:[[9],[3,15],[20],[7]]
解释:
列 -1 :只有结点 9 在此列中。
列 0 :只有结点 3 和 15 在此列中,按从上到下顺序。
列 1 :只有结点 20 在此列中。
列 2 :只有结点 7 在此列中。
示例 2:
输入:root = [1,2,3,4,5,6,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
列 -2 :只有结点 4 在此列中。
列 -1 :只有结点 2 在此列中。
列 0 :结点 1 、5 和 6 都在此列中。
1 在上面,所以它出现在前面。
5 和 6 位置都是 (2, 0) ,所以按值从小到大排序,5 在 6 的前面。
列 1 :只有结点 3 在此列中。
列 2 :只有结点 7 在此列中。
示例 3:
输入:root = [1,2,3,4,6,5,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
这个示例实际上与示例 2 完全相同,只是结点 5 和 6 在树中的位置发生了交换。
因为 5 和 6 的位置仍然相同,所以答案保持不变,仍然按值从小到大排序。
1.1.2. 题解:
- 这题看起来简单,其实容易出坑,我一开始就没有注意到 它相同列里 要根据层来排序....
- 这题简单理解,就是不要看题目的"坐标",就理解成每个节点 有个 值, 比如根节点开始, 根节点是0, 它的左子节点是 -1,右子节点是1, 根节点的左子节点的左子节点是 -2,依次类推
- 然后注意一下示例的2和3, 如果是同一高度的同一个 "横坐标",需要进行大小排序,这里注意,不是全部排序,是同一层的同一个 横坐标需要排序
1.1.3. 思路:
- 首先,肯定是 从根节点开始递归,可以中序遍历树, 左节点就减一,右节点就加一
- 然后有个map,记录每层的每个横坐标里的值, 公式 map[层][横坐标的值] = []int{这一层里相同横坐标的节点的值}
- 比如 根节点所在的 0层, map[0][0] = []int{0},
- 比如根节点的左右子节点, 左节点: map[1][-1] = []int{-1}, 右节点: map[1][1] = []int{1}
- 然后把一层里的值进行排序
1.1.4. 代码:
点击显示
func verticalTraversal(root *TreeNode) (res [][]int) {
if root == nil {
return nil
}
// 一个map,存 每层对应相同横坐标的 集合
mn := make(map[int]map[int][]int)
// 匿名函数 遍历二叉树, n是横坐标的值, deep是树高
var f func(t *TreeNode, n, deep int)
// min,max 是 横坐标的最大最小值, deepMax是树最高
var min, max, deepMax int
f = func(t *TreeNode, n, deep int) {
if t == nil {
return
}
// 记录 横坐标的最大最小值
if n > max {
max = n
}
if n < min {
min = n
}
// 记录 树高最大值
if deep > deepMax {
deepMax = deep
}
// 如果是新遍历到这层,需要重新定义一个map
if _, ok := mn[deep]; !ok {
m := make(map[int][]int)
m[n] = append(m[n], t.Val)
mn[deep] = m
} else {
// 把值插入到 同一层的同一个横坐标的里面
mn[deep][n] = append(mn[deep][n], t.Val)
// 我下面自己写了一个排序,也可以用go自带的sort排序,自带的是 快排
//if len(mn[deep][n]) == 0 {
// mn[deep][n] = append(mn[deep][n], t.Val)
//
//} else {
// mn[deep][n] = sort(mn[deep][n], t.Val)
//}
sort2.Ints(mn[deep][n])
}
deep++
f(t.Left, n-1, deep)
f(t.Right, n+1, deep)
}
f(root, 0, 0)
//fmt.Println("====================")
//fmt.Println(min, max, deepMax)
temp := make(map[int][]int)
// 把不同层里的相同横坐标进行合并
for i := 0; i <= deepMax; i++ {
for j := min; j <= max; j++ {
temp[j] = append(temp[j], mn[i][j]...)
}
}
// 我测试看结果的
for k, v := range temp {
fmt.Println(k, v)
}
// 把结果输出出去
for i := min; i <= max; i++ {
res = append(res, temp[i])
}
return res
}
// 自己实现的排序,本来想用二分进行插入,发现条件太多,就改用这种简单冒泡方式了
func sort(arr []int, n int) (res []int) {
//fmt.Println(arr, n)
if len(arr) == 1 {
if arr[0] > n {
res = []int{n, arr[0]}
} else {
res = []int{arr[0], n}
}
return
}
if n <= arr[0] {
res = append([]int{n}, arr...)
return
}
if n >= arr[len(arr)-1] {
res = append(res, n)
}
for i := 0; i < len(arr); i++ {
if n >= arr[i] && n <= arr[i+1] {
res = append(res, arr[:i+1]...)
res = append(res, n)
res = append(res, arr[i+1:]...)
break
}
}
return
}